Плотность
| Плотность | |
|---|---|
| ρ=mV{displaystyle rho ={frac {m}{V}}} | |
| Размерность | L−3 M |
| Единицы измерения | |
| СИ | кг/м³ |
| СГС | г/см³ |
| Примечания | |
скалярная величина | |
Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму[1].
Для обозначения плотности обычно используется греческая буква ρ (ро) (происхождение обозначения подлежит уточнению), иногда используются также латинские буквы D и d (от лат. densitas — «плотность»).
Более точное определение плотности требует уточнение формулировки:
Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
Плотность вещества — это плотность однородного или равномерно неоднородного тела, состоящего из этого вещества.
Плотность тела в точке — это предел отношения массы малой части тела (Δm{displaystyle Delta m}), содержащей эту точку, к объёму этой малой части (ΔV{displaystyle Delta V}), когда этот объём стремится к нулю[2], или, записывая кратко, limΔV→0Δm/ΔV{displaystyle lim _{Delta Vto 0}{Delta m/Delta V}}. При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.
Поскольку масса в теле может быть распределена неравномерно, более адекватная модель определяет плотность в каждой точке тела как производную массы по объёму. Если учитывать точечные массы, то плотность можно определить как меру, либо как производную Радона—Никодима по отношению к некоторой опорной мере.
Содержание
1 Виды плотности и единицы измерения
2 Формула нахождения плотности
3 Зависимость плотности от температуры
4 Диапазон плотностей в природе
5 Плотности астрономических объектов
6 Плотности некоторых газов
7 Плотности некоторых жидкостей
8 Плотность некоторых пород древесины
9 Плотность некоторых металлов
10 Измерение плотности
11 См. также
12 Примечания
13 Литература
14 Ссылки
Виды плотности и единицы измерения |
Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.
Для сыпучих и пористых тел различают:
- истинную плотность, определяемую без учёта пустот;
удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму. Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме. Для сыпучих тел удельная плотность называется насыпно́й плотностью.
Формула нахождения плотности |
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
- ρ=mV,{displaystyle rho ={frac {m}{V}},}
где m — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.
- При вычислении плотности газов при нормальных условиях эта формула может быть записана и в виде:
- ρ=MVm,{displaystyle rho ={frac {M}{V_{m}}},}
- где М — молярная масса газа, Vm{displaystyle V_{m}} — молярный объём (при нормальных условиях приближённо равен 22,4 л/моль).
Плотность тела в точке записывается как
- ρ=dmdV,{displaystyle rho ={frac {dm}{dV}},}
тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как
- m=∫ρ(r)d3r=∫ρ(r)dV=∫dm.{displaystyle m=int rho (mathbf {r} )d^{3}mathbf {r} =int rho (mathbf {r} )dV=int dm.}
Зависимость плотности от температуры |
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.
Диапазон плотностей в природе |
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда (2·10−31—5·10−31 кг/м³, без учёта тёмной материи)[3].
- Плотность межзвёздной среды приблизительно равна 10−23—10−21 кг/м³.
- Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
- Плотность газообразного водорода (самого лёгкого газа) при нормальных условиях равна 0,0899 кг/м³.
- Плотность сухого воздуха при нормальных условиях составляет 1,293 кг/м³.
- Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.- Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
- Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
- Плотность пресной воды при 4 °C 1000 кг/м³.
- Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
Гранит имеет плотность 2600 кг/м³.- Средняя плотность Земли равна 5520 кг/м³.
- Плотность железа равна 7874 кг/м³.
- Плотность металлического урана 19100 кг/м³.
- Плотность атомных ядер приблизительно 2·1017 кг/м³.
- Теоретически верхняя граница плотности по современным физическим представлениям это планковская плотность 5,1⋅1096 кг/м³.
Плотности астрономических объектов |
системы (в г/см³)[4][5][6]
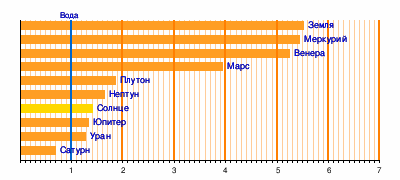
- Средние плотности небесных тел Солнечной системы см. на врезке.
Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.- Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
- Плотность межгалактической среды 2×10−34÷5×10−34 кг/м³.
- Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
- Плотность белых карликов 108÷1012 кг/м³
- Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
- Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:
- ρ=3c632πM2G3.{displaystyle rho ={frac {3,c^{6}}{32pi M^{2}G^{3}}}.}
- Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M−2). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 1019 кг/м³, превышающей ядерную плотность (2×1017 кг/м³), то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).
Плотности некоторых газов |
| Азот | 1,250 | Кислород | 1,429 |
| Аммиак | 0,771 | Криптон | 3,743 |
| Аргон | 1,784 | Ксенон | 5,851 |
| Водород | 0,090 | Метан | 0,717 |
Водяной пар (100 °C) | 0,598 | Неон | 0,900 |
| Воздух | 1,293 | Радон | 9,81 |
| Гексафторид вольфрама | 12,9 | Углекислый газ | 1,977 |
| Гелий | 0,178 | Хлор | 3,164 |
| Дициан | 2,38 | Этилен | 1,260 |
Для вычисления плотности произвольного идеального газа, находящегося в произвольных условиях, можно использовать формулу, выводящуюся из уравнения состояния идеального газа:[7]
ρ=pMRT{displaystyle rho ={frac {pM}{RT}}},
где:
p{displaystyle p} — давление,
M{displaystyle M} — молярная масса,
R{displaystyle R} — универсальная газовая постоянная, равная приблизительно 8,314 Дж/(моль·К)
T{displaystyle T} — термодинамическая температура.
Плотности некоторых жидкостей |
| Бензин | 710 | Молоко | 1040 |
Вода (4 °C) | 1000 | Ртуть (0 °C) | 13600 |
| Керосин | 820 | Диэтиловый эфир | 714 |
| Глицерин | 1260 | Этанол | 789 |
| Морская вода | 1030 | Скипидар | 860 |
| Масло оливковое | 920 | Ацетон | 792 |
| Масло моторное | 910 | Серная кислота | 1835 |
| Нефть | 550—1050 | Жидкий водород (−253 °C) | 70 |
Плотность некоторых пород древесины |
| Бальса | 0,15 | Пихта сибирская | 0,39 |
| Секвойя вечнозелёная | 0,41 | Ель | 0,45 |
| Ива | 0,46 | Ольха | 0,49 |
| Осина | 0,51 | Сосна | 0,52 |
| Липа | 0,53 | Конский каштан | 0,56 |
| Каштан съедобный | 0,59 | Кипарис | 0,60 |
| Черёмуха | 0,61 | Лещина | 0,63 |
| Грецкий орех | 0,64 | Берёза | 0,65 |
| Вишня | 0,66 | Вяз гладкий | 0,66 |
| Лиственница | 0,66 | Клён полевой | 0,67 |
| Тиковое дерево | 0,67 | Бук | 0,68 |
| Груша | 0,69 | Дуб | 0,69 |
Свитения (Махагони) | 0,70 | Платан | 0,70 |
Жостер (крушина) | 0,71 | Тис | 0,75 |
| Ясень | 0,75 | Слива | 0,80 |
| Сирень | 0,80 | Боярышник | 0,80 |
Пекан (кария) | 0,83 | Сандаловое дерево | 0,90 |
| Самшит | 0,96 | Эбеновое дерево | 1,08 |
| Квебрахо | 1,21 | Бакаут | 1,28 |
| Пробка | 0,20 |
Плотность некоторых металлов |
Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.
| Осмий | 22,61[8] | Родий | 12,41[9] | Хром | 7,19[10] |
| Иридий | 22,56[11] | Палладий | 12,02[12] | Германий | 5,32[13] |
| Плутоний | 19,84[14] | Свинец | 11,35[15] | Алюминий | 2,70[16] |
| Платина | 19,59[17] | Серебро | 10,50[18] | Бериллий | 1,85[19] |
| Тантал | 19,30[20] | Медь | 8,94[21] | Цезий | 1,84[22] |
| Золото | 19,30[15] | Никель | 8,91[23] | Рубидий | 1,53[24] |
| Уран | 19,05[25] | Кобальт | 8,86[26] | Натрий | 0,97[27] |
| Ртуть | 13,53[28] | Железо | 7,87[29] | Калий | 0,86[30] |
| Рутений | 12,45[31] | Марганец | 7,44[32] | Литий | 0,53[33] |
Измерение плотности |
Для измерений плотности используются:
Пикнометр — прибор для измерения истинной плотности- Различные виды ареометров — измерители плотности жидкостей.
Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
Этот раздел не завершён. |
См. также |
 Воспроизвести медиафайл
Воспроизвести медиафайлВидеоурок: плотность вещества
Список химических элементов с указанием их плотности- Удельный вес
- Удельная плотность
- Относительная плотность
- Объёмная плотность
- Конденсация
Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.- Концентрация частиц
- Концентрация растворов
- Плотность заряда
- Уравнение неразрывности
Примечания |
↑ Существуют также поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам.
↑ Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
↑ Агекян Т. А. Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
↑ Planetary Fact Sheet (англ.)
↑ Sun Fact Sheet (англ.)
↑ Stern, S. A.; et al. (2015). “The Pluto system: Initial results from its exploration by New Horizons”. Science. 350 (6258): 249—352. DOI:10.1126/science.aad1815..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
↑ МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА. Учебно-методическое пособие к лабораторным работам № 1-51, 1-61, 1-71, 1-72 (неопр.). Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров (2014). Проверено 4 января 2019.
↑ Krebs, 2006, p. 158.
↑ Krebs, 2006, p. 136.
↑ Krebs, 2006, p. 96.
↑ Krebs, 2006, p. 160.
↑ Krebs, 2006, p. 138.
↑ Krebs, 2006, p. 198.
↑ Krebs, 2006, p. 319.
↑ 12 Krebs, 2006, p. 165.
↑ Krebs, 2006, p. 179.
↑ Krebs, 2006, p. 163.
↑ Krebs, 2006, p. 141.
↑ Krebs, 2006, p. 67.
↑ Krebs, 2006, p. 151.
↑ Krebs, 2006, p. 111.
↑ Krebs, 2006, p. 60.
↑ Krebs, 2006, p. 108.
↑ Krebs, 2006, p. 57.
↑ Krebs, 2006, p. 313.
↑ Krebs, 2006, p. 105.
↑ Krebs, 2006, p. 50.
↑ Krebs, 2006, p. 168.
↑ Krebs, 2006, p. 101.
↑ Krebs, 2006, p. 54.
↑ Krebs, 2006, p. 134.
↑ Krebs, 2006, p. 98.
↑ Krebs, 2006, p. 47.
Литература |
Плотность — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
Плотность — статья из Физической энциклопедии. Т. 3, С. 637.- Krebs R. E. The History and Use of Our Earth's Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.
Ссылки |
Онлайн интерактивная таблица плотности веществ (рус.)
Подробная таблица значений плотности распространенных жидкостей (рус.)














