Bdtyk

Множество Мандельброта — классический образец фрактала

Фрактальная форма кочана капусты сорта Романеско (Brassica oleracea)

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Самоподобные фигуры, повторяющиеся конечное число раз, называются предфракталами.

Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференцируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введён Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы». Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.

Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных ниже свойств:

• Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если рассмотреть небольшой фрагмент регулярной фигуры в очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, то есть на всех шкалах можно увидеть одинаково сложную картину.


• Является самоподобным или приближённо самоподобным.


• Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.

Многие объекты в природе обладают свойствами фрактала, например: побережья, облака, кроны деревьев, снежинки, система кровообращения, альвеолы.

Примеры |

Самоподобные множества с необычными свойствами в математике |

Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:

• 
  множество Кантора — нигде не плотное несчётное совершенное множество. Модифицировав процедуру, можно также получить нигде не плотное множество положительной длины;


• 
  треугольник Серпинского («скатерть») и ковёр Серпинского — аналоги множества Кантора на плоскости;


• 
  губка Менгера — аналог множества Кантора в трёхмерном пространстве;


• примеры Вейерштрасса и Ван дер Вардена нигде не дифференцируемой непрерывной функции;


• 
  кривая Коха — несамопересекающаяся непрерывная кривая бесконечной длины, не имеющая касательной ни в одной точке;


• 
  кривая Пеано — непрерывная кривая, проходящая через все точки квадрата;


• траектория броуновской частицы также с вероятностью 1 нигде не дифференцируема. Её хаусдорфова размерность равна двум^{[источник не указан 2217 дней]}.

Рекурсивная процедура получения фрактальных кривых |

Построение кривой Коха

Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены первый, второй и четвёртый шаги этой процедуры для кривой Коха.

Примерами таких кривых служат:

• 
  кривая Коха (снежинка Коха),


• 
  кривая Леви,


• 
  кривая Минковского,


• Кривая Гильберта


• 
  Ломаная (кривая) дракона (Фрактал Хартера-Хейтуэя),


• 
  кривая Пеано.


• Кривая Мякишева

С помощью похожей процедуры получается дерево Пифагора.

Фракталы как неподвижные точки сжимающих отображений |

Свойство самоподобия можно математически строго выразить следующим образом. Пусть ψi,i=1,…,n{displaystyle psi _{i},,i=1,dots ,n} — сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости:
Ψ:K↦∪i=1nψi(K){displaystyle Psi colon Kmapsto cup _{i=1}^{n}psi _{i}(K)}

Можно показать, что отображение Ψ{displaystyle Psi } является сжимающим отображением на множестве компактов с метрикой Хаусдорфа. Следовательно, по теореме Банаха, это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.

Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения ψi,i=1,…,n{displaystyle psi _{i},,i=1,dots ,n} — отображения подобия, а n{displaystyle n} — число звеньев генератора.

Для треугольника Серпинского n=3{displaystyle n=3} и отображения ψ1{displaystyle psi _{1}}, ψ2{displaystyle psi _{2}}, ψ3{displaystyle psi _{3}} — гомотетии с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении Ψ{displaystyle Psi }.

В случае, когда отображения ψi{displaystyle psi _{i}} — преобразования подобия с коэффициентами ri>0{displaystyle r_{i}>0}, размерность s{displaystyle s} фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения r1s+r2s+⋯+rns=1{displaystyle r_{1}^{s}+r_{2}^{s}+dots +r_{n}^{s}=1}. Так, для треугольника Серпинского получаем s=ln⁡3/ln⁡2{displaystyle s=ln 3/ln 2}.

По той же теореме Банаха, начав с любого компактного множества и применяя к нему итерации отображения Ψ{displaystyle Psi }, мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.

Фракталы в комплексной динамике |

Множество Жюлиа́

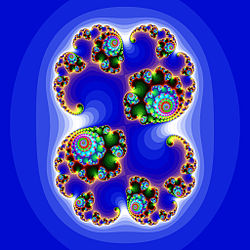
Ещё одно множество Жюлиа

Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу 20 века и связаны с именами Фату и Жюлиа.

Пусть F(z){displaystyle F(z)} — многочлен, z0{displaystyle z_{0}} — комплексное число. Рассмотрим следующую последовательность: z0,z1=F(z0),z2=F(F(z0))=F(z1),z3=F(F(F(z0)))=F(z2),...{displaystyle z_{0},z_{1}=F(z_{0}),z_{2}=F(F(z_{0}))=F(z_{1}),z_{3}=F(F(F(z_{0})))=F(z_{2}),...}

Нас интересует поведение этой последовательности при стремлении n{displaystyle n} к бесконечности. Эта последовательность может:

• стремиться к бесконечности,


• стремиться к конечному пределу,


• демонстрировать в пределе циклическое поведение, например: z1,z2,z3,z1,z2,z3,...{displaystyle z_{1},z_{2},z_{3},z_{1},z_{2},z_{3},...}
  


• вести себя хаотично, то есть не демонстрировать ни один из трёх упомянутых типов поведения.

Множества значений z0{displaystyle z_{0}}, для которых последовательность демонстрирует один конкретный тип поведения, а также множества точек бифуркации между различными типами, часто обладают фрактальными свойствами.

Так, множество Жюлиа — множество точек бифуркации для многочлена F(z)=z2+c{displaystyle F(z)=z^{2}+c} (или другой похожей функции), то есть тех значений z0{displaystyle z_{0}}, для которых поведение последовательности zn{displaystyle z_{n}} может резко меняться при сколь угодно малых изменениях z0{displaystyle z_{0}}.

Другой вариант получения фрактальных множеств — введение параметра в многочлен F(z){displaystyle F(z)} и рассмотрение множества тех значений параметра, при которых последовательность zn{displaystyle z_{n}} демонстрирует определённое поведение при фиксированном z0{displaystyle z_{0}}. Так, множество Мандельброта — это множество всех c∈C{displaystyle cin mathbb {C} }, при которых zn{displaystyle z_{n}} для F(z)=z2+c{displaystyle F(z)=z^{2}+c} и z0{displaystyle z_{0}} не стремится к бесконечности.

Ещё один известный пример такого рода — бассейны Ньютона.

Популярно создание красивых графических образов на основе комплексной динамики путём раскрашивания точек плоскости в зависимости от поведения соответствующих динамических систем. Например, для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления zn{displaystyle z_{n}} к бесконечности (определяемой, скажем, как наименьший номер n{displaystyle n}, при котором |zn|{displaystyle |z_{n}|} превысит фиксированную большую величину A{displaystyle A}).

Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.

Стохастические фракталы |

Рандомизированный фрактал на основе множества Жюлиа

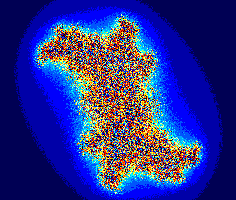
Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:

• траектория броуновского движения на плоскости и в пространстве;


• граница траектории броуновского движения на плоскости. В 2001 году Лоулер, Шрамм и Вернер доказали предположение Мандельброта о том, что её размерность равна 4/3.


• эволюции Шрамма-Лёвнера — конформно-инвариантные фрактальные кривые, возникающие в критических двумерных моделях статистической механики, например, в модели Изинга и перколяции.


• различные виды рандомизированных фракталов, то есть фракталов, полученных с помощью рекурсивной процедуры, в которую на каждом шаге введён случайный параметр. Плазма — пример использования такого фрактала в компьютерной графике.

Природные объекты, обладающие фрактальными свойствами |

Вид спереди на трахею и бронхи

Природные объекты (квазифракталы) отличаются от идеальных абстрактных фракталов неполнотой и неточностью повторений структуры. Большинство встречающихся в природе фракталоподобных структур (границы облаков, линия берега, деревья, листья растений, кораллы, …) являются квазифракталами, поскольку на некотором малом масштабе фрактальная структура исчезает. Природные структуры не могут быть идеальными фракталами из-за ограничений, накладываемых размерами живой клетки и, в конечном итоге, размерами молекул.

• В живой природе:
  
  
  
  • Кораллы
  
  
  • 
    Морские звезды и ежи
    
  
  
  • Морские раковины
  
  
  • Цветы и растения (брокколи, капуста)
  
  
  • Кроны деревьев и листья растений
    
  
  
  • Плоды (ананас)
  
  
  • 
    Система кровообращения и бронхи людей и животных
  
  
  
  


• В неживой природе:
  
  
  
  • 
    Границы географических объектов (стран, областей, городов)
  
  
  • Береговые линии
  
  
  • Горные хребты
  
  
  • Снежинки
  
  
  • Облака
  
  
  • Молнии
  
  
  • Морозные узоры на оконных стёклах
    
  
  
  • Кристаллы
  
  
  • 
    Сталактиты, сталагмиты, геликтиты.
  
  
  
  

Применение |

Естественные науки |

В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и тому подобное. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов). После создания кривой Коха было предложено использовать её при вычислении протяжённости береговой линии.

Радиотехника |

Фрактальные антенны |

Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику.

Коэн основал собственную компанию и наладил серийный выпуск своих антенн. C тех пор теория фрактальных антенн продолжает интенсивно развиваться.
^[1][2][3]
Преимуществом таких антенн является многодиапазонность и сравнительная широкополосность.

Информатика |

Сжатие изображений |

Фрактальное дерево

Существуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранить сжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован^[4] фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.

Компьютерная графика |

Ещё одно фрактальное дерево

Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, см. Генератор фракталов (программа).

Децентрализованные сети |

Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.

Галерея |

См. также |

• Красота математики


• Множество Мандельброта


• Множество Жюлиа


• Бассейны (фракталы) Ньютона


• Биоморфы


• Круговой фрактал


• Мультифрактал


• Алгоритм фрактального сжатия


• Теорема о рекурсивных системах


• Фрактальная гомогенность


• Измерение длины береговой линии


• Фрактальный кластер

Примечания |

Литература |

• А. А. Кириллов. Повесть о двух фракталах. — Летняя школа «Современная математика». — Дубна, 2007.


• Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.


• Пайтген Х.-О., Рихтер П. Х. Красота фракталов. Образы комплексных динамических систем. — М.: «Мир», 1993.


• Федер Е. Фракталы. — М: «Мир», 1991.


• Абачиев С. К. О треугольнике Паскаля, простых делителях и фрактальных структурах // В мире науки, 1989, № 9.


• 
  Фоменко А. Т. Наглядная геометрия и топология. — М.: изд-во МГУ, 1993.


• 
  Цицин Ф. А. Фрактальная вселенная // «Дельфис» — № 11(3) — 1997.


• Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике, 1985. — М.: «Мир», 1988.


• 
  Маврикиди Ф. И. Фракталы: постигая взаимосвязанный мир // «Дельфис» — № 23(3) — 2000.


• Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. — Ижевск: «РХД», 2001.


• Кроновер Р. М. Фракталы и хаос в динамических системах. Основы теории.


• Мандельброт Бенуа, Ричард Л. Хадсон. (Не)послушные рынки: фрактальная революция в финансах = The Misbehavior of Markets. — М.: «Вильямс», 2006. — 400 с. — ISBN 5-8459-0922-8.


• Красивая жизнь комплексных чисел // Hard’n’Soft, № 9, 2002. Стр. 90.


• М. Г. Иванов, «Размер и размерность» // «Потенциал», август 2006.


• 
  Маврикиди Ф. И. Фрактальная математика и природа перемен // «Дельфис» — № 54(2) — 2008.


• Липов А.Н. Фракталы. Памяти Бенуа Мандельброта // Философия и культура № 9 (33) 2010. № 8. С. 39-54.

Ссылки |

	Фрактал на Викискладе

• 
  Фракталы в простых числах — Статья Сергея Герасимова на habrahabr
  


• 
  Статья о фракталах. Приведены примеры расчета и построения графической интерпретации некоторых алгебраических и геометрических фракталов. Имеются ссылки на онлайн генераторы и исходные коды на C#.


• Надежда Атаева, Фрактальные множества (Санкт-Петербургский государственный университет: ПМ-ПУ)


• 
  Обаяние самоподобия. Лампочка Мандельброта и многое другое в галерее фракталов от Ленты. Ру // Лента. Ру, 27 фото.


• 
  Фракталы — геометрия природы. Реализация фракталов в delphi и многое другое в Клубе программистов.


• «Фракталы. Поиски новых размерностей» (англ. Fractals. Hunting The Hidden Dimension) — научно-популярный фильм, снятый в 2008 г.


• 
  Фракталы на Элементы.ру
  


• J. J. O'Connor, E. F. Robertson. A History of Fractal Geometry (неопр.). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland (февраль 2009).